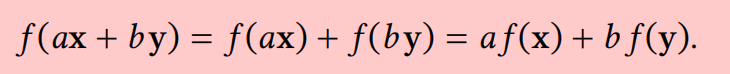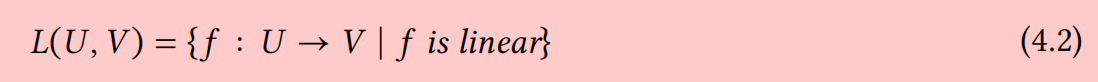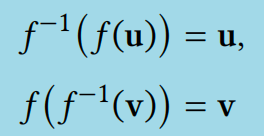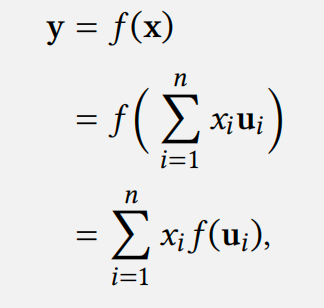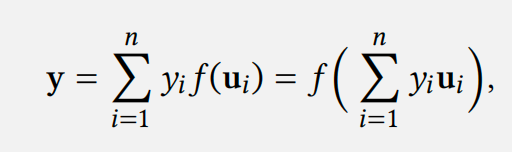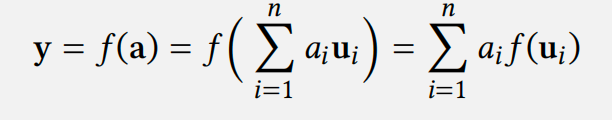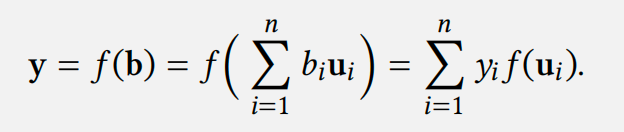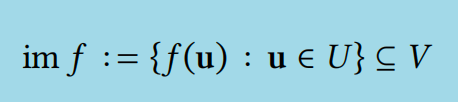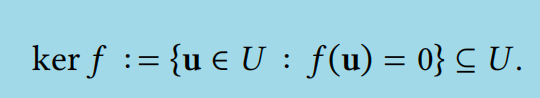机器学习的数学基础-线性变换(一)

在大多数线性代数课程中，矩阵是课程的核心。而在机器学习中，我们则始终与矩阵打交道。问题是：矩阵并不能说明一切。仅仅看矩阵很难理解其中的规律。例如，为什么矩阵乘法的定义如此复杂？为什么像$𝐵 = 𝑇^{−1}𝐴𝑇$这样的关系很重要？为什么有些矩阵可逆，而有些则不可逆？

为了真正理解其中的奥秘，我们必须探究矩阵的起源：线性变换。

本文的主要内容包括：

什么是线性变换？
线性变换和矩阵
矩阵运算回顾
逆线性变换
核与像

“我的眼睛为什么会痛？” “你以前从来没用过。” ——莫菲斯第一次从“母体”醒来时对尼奥说

我们必须探究矩阵的起源：线性变换。就像尼奥一样，理解其中的奥秘可能会有点痛苦，但它会在以后给我们带来巨大的回报。让我们开始吧！

1 什么是线性变换？

随着内积、正交性和正交/标准正交基的引入，我们对特征空间的结构有了全面的了解。然而，在机器学习中，我们的兴趣主要在于数据的变换。

从这个角度来看，神经网络只是一个由更小的部分（称为层）组成的函数，每一步都将数据变换到一个新的特征空间。线性变换是机器学习模型的关键组成部分之一。

你可能见过形式为𝑓 (𝐱) = 𝐴𝐱的函数，但这只是看待它们的其中一种方式。本节将从几何角度开始，然后转向你可能已经熟悉的代数表示。为了理解神经网络如何学习强大的高级数据表示，了解变换的几何学至关重要。

那么，什么是线性变换？让我们不要犹豫，立即进入定义！

定义 4.1.1（线性变换）

设 𝑈 和 𝑉 是两个向量空间（在同一个标量场上），𝑓 ∶ 𝑈 → 𝑉 是它们之间的函数。如果满足以下条件，则称 𝑓 是线性的

对所有向量 𝐱、𝐲 ∈ 𝑈 和所有标量 𝑎、𝑏成立。

这就是线性代数被称为线性代数的原因。本质上，线性变换是两个向量空间之间的映射，它保留了代数结构：加法和标量乘法。（向量空间之间的函数通常被称为变换，因此我们将使用这个术语。）

备注 4.1.1 线性本质上是将两个性质合二为一：对于所有向量 𝐱、𝐲 和所有标量 𝑎，𝑓 (𝐱 + 𝐲) = 𝑓 (𝐱) + 𝑓 (𝐲) 和 𝑓 (𝑎𝐱) = 𝑎𝑓 (𝐱)。由此可知 (4.1)可进一步写成

从定义中可以立即看出两个性质。首先，由于

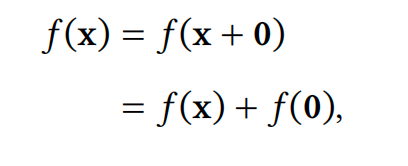
𝑓 (𝟎) = 𝟎 对每个线性变换都成立。此外，线性变换的复合仍然是线性的，正如

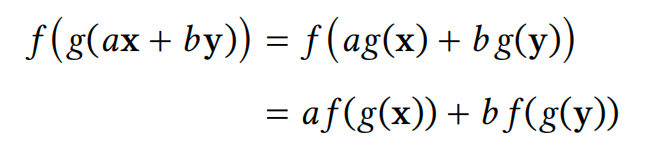
显示了任何线性 𝑓 和 𝑔 以及标量 𝑎 和 𝑏。

像往常一样，让我们看一些例子来建立直觉。

例 1. 对于任何标量 𝑐，缩放变换 𝑓 (𝐱) = 𝑐𝐱 是线性的

这可能是最简单的例子，它可以在所有向量空间中定义。

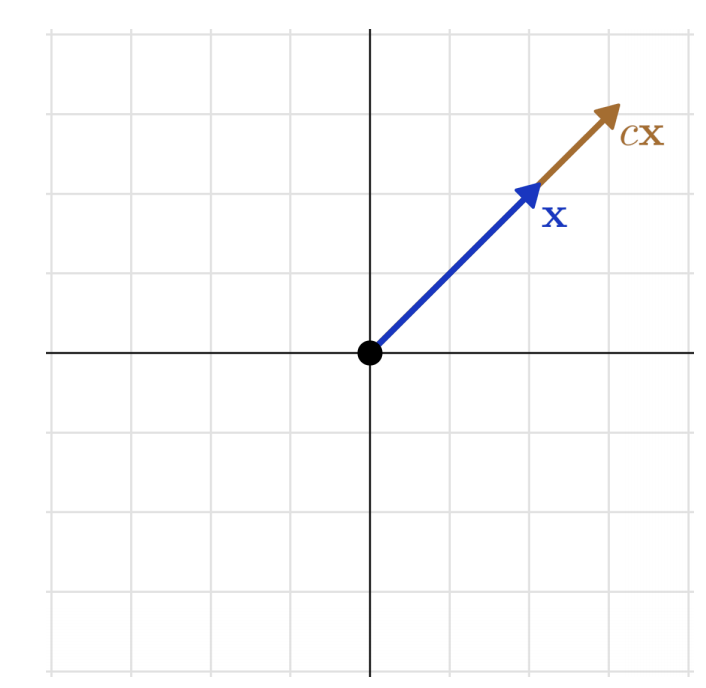
图 4.1：缩放作为线性变换

很容易看出缩放是线性的：

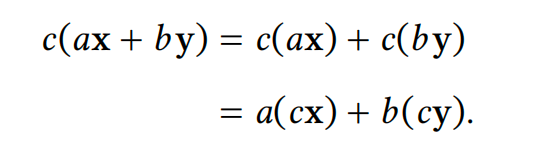
例 2. 在$ℝ^2$中，绕原点旋转𝛼角度也是线性的

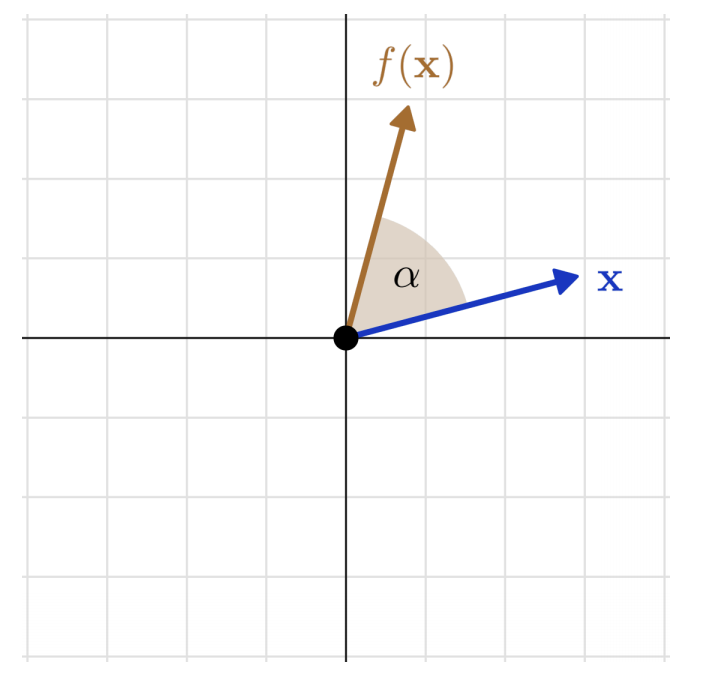
图 4.2：欧氏平面中的旋转作为线性变换

为了证明旋转确实是线性的，我们先直接看一个定义：平面向量$𝐱 = (𝑥_1, 𝑥_2)$ 的旋转角为 𝛼，其表达式为

由 (4.1) 式很容易得到证明。我知道这看起来有点突然，但相信我，旋转公式将会详细解释。你可以用一些基本的三角学知识来解释，或者等到我们稍后用矩阵来解释。

一般来说，线性变换与空间几何有着密切的联系。稍后，我们将详细研究$ℝ^2$的线性变换，重点关注像这样的几何变换。（注意，旋转在高维空间中会稍微复杂一些，因为它们需要一个旋转轴。）

例3：在任何向量空间𝑉和非零向量𝐯∈𝑉中，由𝑓 (𝐱) = 𝐱 + 𝐯定义的平移不是线性的，正如𝑓 (𝟎) = 𝐯 ≠ 𝟎。

我们将在本节后面看到更多示例。现在，我们来讨论线性变换的一些一般性质。对于任何线性变换 𝑓 ∶ 𝑈 → 𝑉，图像

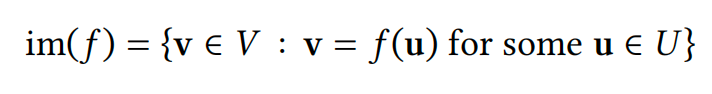
始终是𝐕的子空间（参见第 1.2.7 节）。这很容易验证：如果 $𝐯_1, 𝐯_2 ∈ im 𝑓$，则存在 $𝐮_1, 𝐮_2 ∈ 𝑈$，使得 $𝑓 (𝐮_1) = 𝐯1$ 且 $𝑓 (𝐮_2) = 𝐯_2$，如下式所示

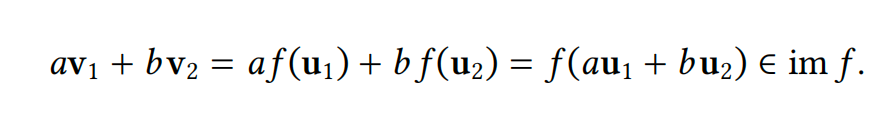
为了增加一个抽象层次，我们将看到所有线性变换的集合形成一个向量空间。

定理 4.1.1 设 𝑈 和 𝑉 是同一域 𝐹 上的两个向量空间。则所有线性变换的集合

也是 𝐹 上的向量空间，具有函数加法和标量乘法的通常定义。

它的证明只是一个枯燥的清单，只是简单回顾了向量空间定义（定义 1.1.1）中的各项内容。我建议你至少过一遍，巩固一下对向量空间的理解，但其实没什么特别的。

1.1 线性变换和矩阵

正如我们所见，线性变换的定义有点抽象。然而，有一种简单而富有表现力的方法来刻画它们。

为了说明这一点，设 𝑓 ∶ 𝑈 → 𝑉 是两个向量空间 𝑈 和 𝑉 之间的线性变换。假设$\{𝐮_1, … , 𝐮_𝑚\}$ 是 𝑈 中的基，而 $\{𝐯_1, … , 𝐯_𝑛\}$ 是 𝑉 中的基。由于每个 𝐱 ∈ 𝑈 都可以写成如下形式

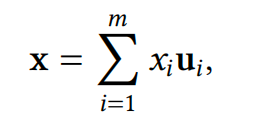
𝑓 的线性意味着

这意味着$𝑓 (𝐱)$ 是$𝑓 (𝐮_1), … , 𝑓 (𝐮_𝑚)$ 的线性组合。换句话说，每个线性变换都完全由基向量的像决定。为了扩展这个想法，假设对于每个$𝐮_𝑗$，对于某些标量$𝑎_{𝑖,𝑗}$，我们有

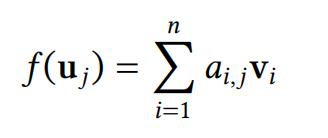
这些𝑛 × 𝑚 数完全描述了𝑓。为了符号简单，我们将它们存储在一个𝑛 × 𝑚 大小的表中，称为矩阵，我们将其表示为$𝐴_𝑓$：

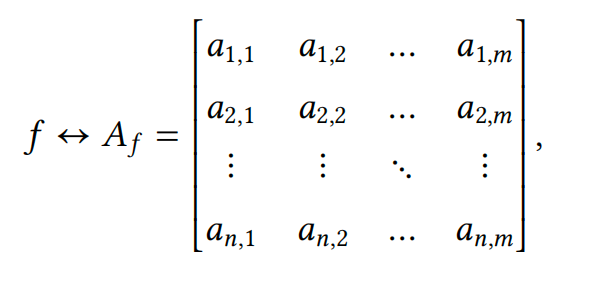
这意味着线性变换可以用矩阵来表示。这种联系在机器学习中被广泛应用。

进一步展开（4.3），对于每个$𝐱 = ∑^𝑚_{𝑗=1} 𝑥_𝑗𝐮_𝑗$，我们有

因此，𝐱 的图像可以表示为$𝐴_𝑓 𝐱$：

这里需要注意两点。首先，我们隐式地选择将向量表示为列而不是行。这是一个影响深远的决定，将影响本书后面的许多计算。我们会继续指出这一点。

其次，矩阵表示取决于基的选择！假设$𝑃 = \{𝐩_1, … , 𝐩_𝑛\} ⊂ 𝑈$ 是矩阵的基，我们将这种依赖关系表示为下标，写作$𝐴_{𝑓,𝑃}$。

为了避免混淆，我们几乎只用标准正交基来定义线性变换。在实际场景中，这更容易理解正在发生的事情。所以，每当我写下“设𝐴是线性变换𝑓的矩阵”这样的话，就隐含地假设了𝐴的基函数形式为$𝐞_1 = (1, 0, … , 0), 𝐞_2 = (0, 1, … , 0), … , 𝐞_𝑛 = (0, 0, … , 1)$。

从哲学角度来说，你听说过柏拉图的洞穴寓言吗？在这个思想实验中，人们被假设生活在一个洞穴中，始终面朝一面墙，只能观察身后火焰投射的影子。他们所观察到的并用来构建世界内部表征的东西，与现实截然不同。将这个类比应用到线性代数中，矩阵就是我们在实际场景中观察和使用的影子。在许多入门课程中，线性变换是隐藏的，只教授矩阵微积分。我第一次接触这个主题的经历也类似：我上的第一门线性代数课就只讲矩阵。这门课复杂得令人困惑，简直是数学课里最复杂的了。（我可以向你保证，这门课确实非常复杂和令人困惑。）后来，当我发现可以从线性变换的角度来看待矩阵时，一切都豁然开朗了。

不了解矩阵背后的原理，就不可能掌握线性代数。如果你觉得我的方法太抽象，请记住：多年以后，当你成为一名实践数据科学家/机器学习工程师/研究员或其他任何职位时，深入研究这些原理将会带来巨大的回报。

让我们回到正题，继续讨论线性变换。最常用的矩阵是恒等变换 id ∶ 𝐱 ↦ 𝐱 的矩阵。我们将其表示为 𝐼。很容易看出

总而言之，对于矩阵 𝐴，线性变换可以通过 𝐱 ↦ 𝐴𝐱 给出。实际上，映射

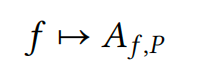
定义了由 (4.2) 定义的线性变换空间 𝐿(𝑈, 𝑉) 与 𝑛 × 𝑚 矩阵集之间的一一对应关系，其中 𝑛 和 𝑚 是对应的维度。

1.2 矩阵运算回顾

函数可以相加和复合。由于线性变换和矩阵之间的联系，矩阵运算继承自相应的函数运算。

基于这一原则，我们定义了矩阵加法，使得两个线性变换之和的矩阵等于对应矩阵之和。

从数学上讲，如果 𝑓 , 𝑔 ∶ 𝑈 → 𝑉 是两个带矩阵的线性变换，𝑓 ↔︎ 𝐴 和 𝑔 ↔︎ 𝐵，那么

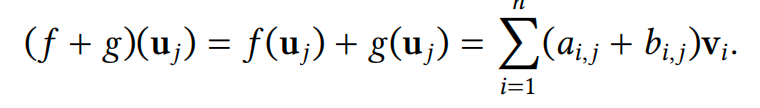
因此，相应的矩阵可以按元素相加：

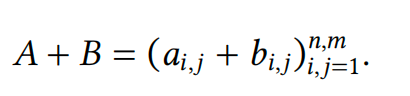
矩阵之间的乘法由相应变换的组合来定义。

为了弄明白如何操作，我们先研究一个特殊情况。（一般来说，先研究特殊情况是个好主意，因为它们通常可以降低复杂性，并让你在不造成信息过载的情况下发现规律。）因此，设 𝑓 , 𝑔 ∶ 𝑈 → 𝑈 为两个线性变换，将 𝑈 映射到自身上。为了确定与𝑓 ◦ 𝑔 对应的矩阵元素，我们必须用所有基向量 $𝐮_1, … , 𝐮_𝑛$ 来表示 $𝑓 (𝑔(𝐮_𝑗))$。为此，我们有

考虑我们如何定义变换矩阵，标量$ (∑^𝑛_{𝑘=1} 𝑎_{𝑖,𝑘}𝑏_{𝑘,𝑗}) $是 𝑓 ◦ 𝑔 矩阵第 𝑖 行第 𝑗 列的元素。因此，矩阵乘法可以定义为

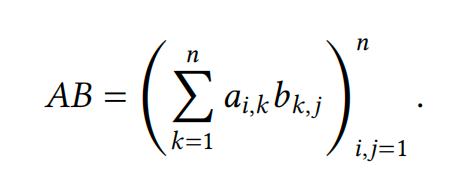
一般情况下，只有当相应的线性变换可以组合时，我们才能定义矩阵的乘积。也就是说，如果𝑓 ∶ 𝑈 → 𝑉，则𝑔 必须从𝑉开始。将其转化为矩阵的语言，𝐴 的列数必须与𝐵 的行数匹配。因此，对于任何$𝐴 ∈ ℝ^{𝑛×𝑚}$ 和$𝐵 ∈ ℝ^{𝑚×𝑙}$，它们的乘积定义为

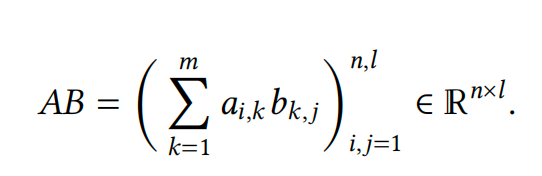
1.3 逆线性变换

对于线性变换，可逆性问题非常重要。例如，你遇到过这样的方程组吗？

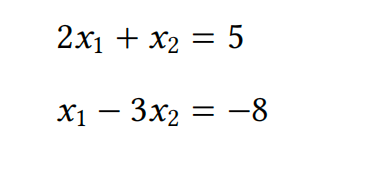
如果我们定义

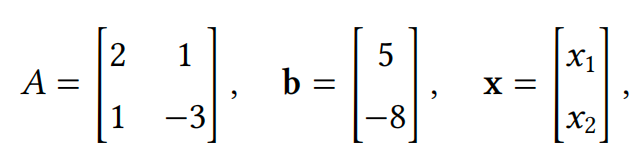
上述系统可以写成𝐴𝐱 = 𝐛的形式。这些被称为线性方程，用于建模从金融到生物学的各种过程。你会如何写出这样一个方程的解？如果存在一个矩阵$𝐴^{-1}$，使得$𝐴^{-1}𝐴$是单位矩阵𝐼（由(4.4)式定义），那么将方程𝐴𝐱 = 𝐛从左乘以$𝐴^{-1}$，将得到$𝐱 = 𝐴^{-1}𝐛$形式的解。

矩阵$𝐴^{-1}$被称为𝐴的逆矩阵。它可能并不总是存在，但当它存在时，由于多种原因，它极其重要。我们稍后会讨论线性方程，但首先，让我们学习一下可逆性的基础知识！以下是一般定义。

定义 4.1.2（线性变换的逆）

设 𝑓 ∶ 𝑈 → 𝑉 是向量空间 𝑈 和 𝑉 之间的线性变换。如果存在一个线性变换 $𝑓^{-1}$ 使得 $𝑓^{-1}◦ 𝑓$ 和 $𝑓 ◦ 𝑓^{-1}$ 为恒等函数，则称 𝑓 可逆；即

对所有𝐮∈𝑈、𝐯∈𝑉成立。 $𝑓^{-1}$称为𝑓的逆。

并非所有线性变换都是可逆的。例如，如果𝑓将所有向量映射到零向量，则无法定义逆变换。

逆变换的存在需要满足某些条件。其中最重要的一个条件是将基的概念与可逆性联系起来。

定理 4.1.2（线性变换的可逆性）

设 𝑓 ∶ 𝑈 → 𝑉 为线性变换，$𝐮_1, … , 𝐮_𝑛$ 为 𝑈 中的基。则 𝑓 可逆当且仅当$𝑓 (𝐮_1), … , 𝑓 (𝐮_𝑛) $为 𝑉 中的基。

以下证明很简单，但可能有点让人一时无法接受。第一次阅读时可以跳过，以后可以随时重新阅读。

证明。与往常一样，“当且仅当"这类定理的证明由两部分组成，因为这些命题涉及两个蕴涵式。

首先，我们证明𝑓可逆，则$𝑓 (𝐮_1), … , 𝑓 (𝐮_𝑛) $是一个基。也就是说，我们需要证明$𝑓 (𝐮_1), … , 𝑓 (𝐮_𝑛)$ 线性无关，且每个𝐲 ∈ 𝑉都可以写成它们的线性组合。由于𝑓可逆，𝑓 (𝟎) = 𝟎，而且不存在非零向量𝐱 ∈ 𝑈 使得𝑓 (𝐱) = 𝟎。换句话说，𝟎 不能写成 $𝑓 (𝐮_1), … , 𝑓 (𝐮_𝑛) $的非平凡线性组合，由此定理 1.2.2推断出它们之间的线性独立性。

另一方面，可逆性意味着每个 𝐲 ∈ 𝑉 都可以表示为 𝐲 = 𝑓 (𝐱)，其中 𝐱 ∈ 𝑈。（假设 $𝐱 = 𝑓^{−1}(𝐲)$。）由于 $𝐮_1, … ，𝐮_𝑛 $是一个基，$𝐱 = ∑^𝑛_{𝑖=1} 𝑥_𝑖𝐮_𝑖$。因此，

可以证明 $span(𝑓 (𝐮_1), … , 𝑓 (𝐮_𝑛)) = 𝑉$。

$𝑓 (𝐮_1), … , 𝑓 (𝐮_𝑛) $的线性独立性以及它张成 𝑉 的事实表明它确实是基。

现在我们证明另一个蕴涵式：如果 $𝑓 (𝐮_1), … , 𝑓 (𝐮_𝑛)$ 是基，则 𝑓 可逆。

如果$ 𝑓 (𝐮_1), … , 𝑓 (𝐮_𝑛) $确实是基，则每个 𝐲 ∈ 𝑉 都可以写成

这证明了全射性。关于单射性，如果对于某个𝐚，𝐛∈𝑈，𝐲 = 𝑓 (𝐚) = 𝑓 (𝐛)，那么，由于𝐚 和 𝐛 都可以写成$𝐮_𝑖$基向量的线性组合，因此我们有

和

因此，$𝟎 = ∑^𝑛_{𝑖=1}(𝑎_𝑖 − 𝑏_𝑖)𝐮_𝑖$，且由于$𝐮_1, … , 𝐮_𝑛 $是 U 中的一个基，$𝑎_𝑖 = 𝑏_𝑖$ 必定成立。因此𝑓 是单射。

该定理的一个推论是，如果𝑈和𝑉的维数不同，则线性变换𝑓 ∶ 𝑈 → 𝑉不可逆。我们也可以从矩阵的角度来看待可逆性。对于任何$𝐴 ∈ ℝ^{𝑛×𝑛}$，如果相应的线性变换可逆，则存在一个矩阵$𝐴^{−1} ∈ ℝ^{𝑛×𝑛}$使得$𝐴^{−1}𝐴 = 𝐴𝐴^{−1} = 𝐼$。如果一个矩阵不是方阵，那么它在经典意义上不可逆。

1.4 核与像

关于线性变换的可逆性，有两个特殊的集合起着至关重要的作用：核和像。让我们来看一下！

定义 4.1.3（线性变换的核和像）

设 𝑓 ∶ 𝑈 → 𝑉 为线性变换。其像和核定义为

和

通常，我们将某个矩阵 𝐴 写为 im 𝐴 和 ker𝐴，指的是由 𝐱 ↦ 𝐴𝐱 定义的线性变换。

由于 𝑓 的线性性，很容易看出 im 𝑓 是 𝑉 的子空间，而 ker 𝑓 是 𝑈 的子空间。如上所述，它们与可逆性密切相关，我们接下来会看到。

定理 4.1.3（线性变换的可逆性）

设 𝑓 ∶ 𝑈 → 𝑉 为线性变换。

（a）𝐴 为单射当且仅当 ker 𝑓 = {𝟎}。

（b）𝐴 为全射当且仅当 im 𝑓 = 𝑉。

（c）𝐴 为双射（即可逆），当且仅当 ker 𝑓 = {𝟎} 且 im 𝑓 = 𝑉。

证明：(a) 如果 𝑓 是单射，则 𝑈 中只能有一个向量映射到 𝟎。由于对于任何线性变换，𝑓 (𝟎) = 𝟎，因此 ker 𝑓 = {𝟎}。另一方面，如果有两个不同的向量 𝐱，𝐲 ∈ 𝑈，使得 𝑓 (𝐱) = 𝑓 (𝐲)，则 𝑓 (𝐱 − 𝐲) =𝑓 (𝐱) − 𝑓 (𝐲) = 𝟎，因此 𝐱 − 𝐲 ∈ ker 𝑓。因此，ker 𝑓 = {𝟎} 蕴涵 𝐱 = 𝐲，从而给出单射性。（b）这只是全射性的定义。

（c）这是由上面（a）和（b）的结合立即得出的。

因为矩阵定义了线性变换，所以讨论矩阵的逆是有意义的。

从代数角度来说，$𝐴 ∈ ℝ^{𝑛×𝑛}$的逆是矩阵$𝐴^{−1} ∈ ℝ^{𝑛×𝑛}$，使得$𝐴^{−1}𝐴 = 𝐴𝐴^{−1} = 𝐼$成立。线性变换和矩阵之间的联系意味着$𝐴^{−1}$ 是$𝑓^{−1}$的矩阵，所以这并不奇怪。

如果本节关于可逆性的内容感觉涉及太多代数，不用担心。稍后，在讨论变换的行列式时，我们将在本章后面从几何角度研究可逆性。关于矩阵，稍后我们将在5.1.6节中看到计算逆矩阵的通用方法。我们很快就会讲到这一点，但首先，我们先来看看基的选择如何决定矩阵的表示。