本文是基于《深度学习中的数学》一书中的思想,旨在从本文起系列阐述深度学习技术背后的数学原理,给想要对深度学习更进一步了解的读者提供一个可以查阅的底层原理资料。本文共分为四个部分,此为第四部分。
本文的主要内容包括:
- 线性和非线性模型
- 通过多个非线性层实现更高的表达能力:深度神经网络
1.6 线性和非线性模型
在图1.2中,我们面临一个相当简单的情况,即类别可以用一条线(高维曲面中的超平面)分隔。这在现实生活中并不常见。如果不同类别的点无法用一条线分开,如图1.4所示,该怎么办?在这种情况下,我们的模型架构不应再是简单的加权组合。它应是一个非线性函数。例如,请看图1.4中的曲线分隔符。从函数逼近的角度来看,非线性模型也是有意义的。最终,我们的目标是近似非常复杂且高度非线性的函数,以模拟生活中所需的分类或估计过程。直观地说,使用非线性函数来建模它们似乎会更好。
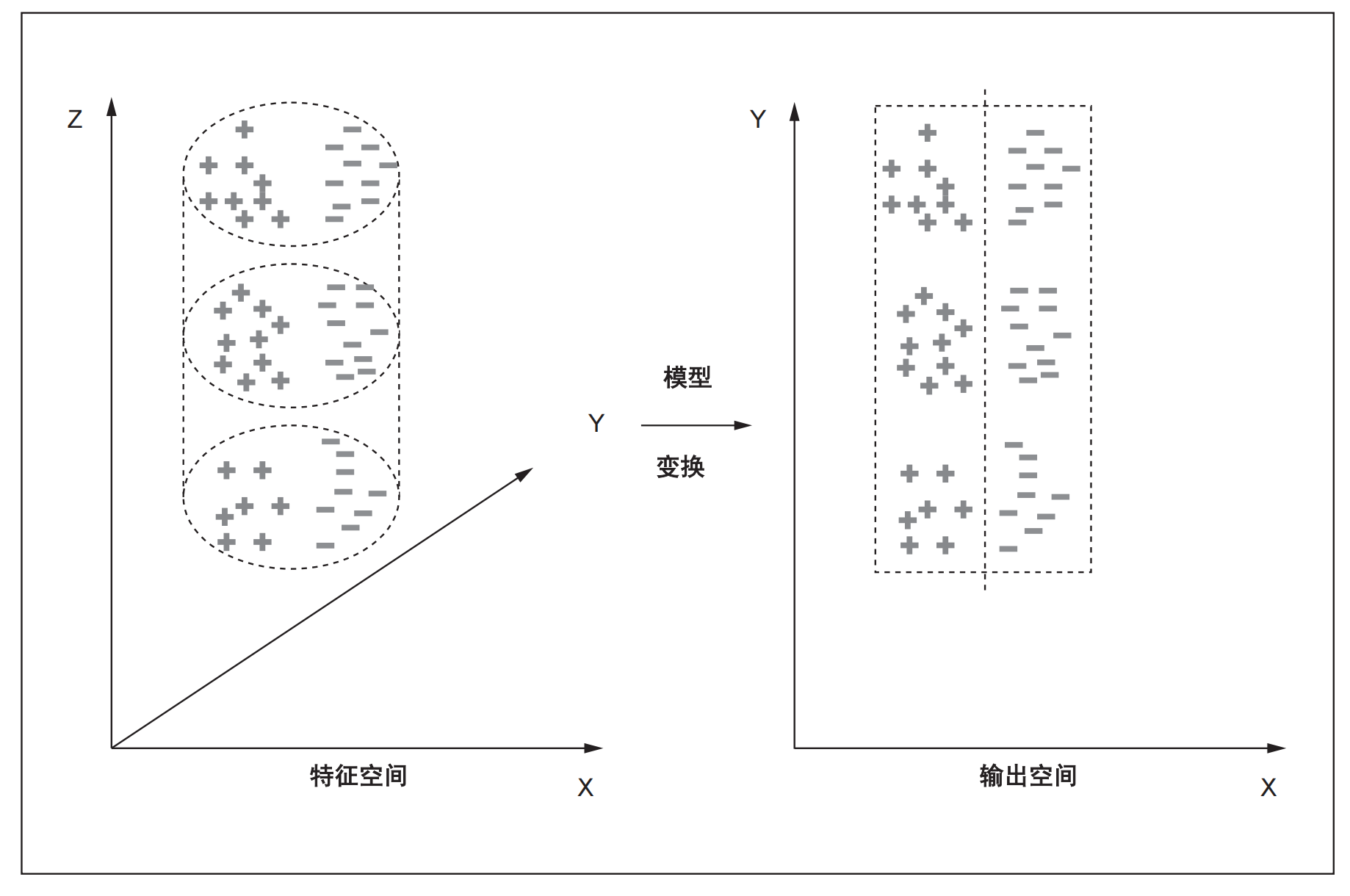
图1.3 模型将输入(特征)空间中的点映射到输出空间,在输出空间中更容易进行类别划分。例如,在该图中,属于两个类(红色(+)和绿色(-))的输入特征点分布在三维特征空间中的圆柱体体积上。该模型将圆柱体展开为矩形。特征点被映射到二维平面输出空间,在输出空间中,可以使用简单的线性分离器区分这两个类。
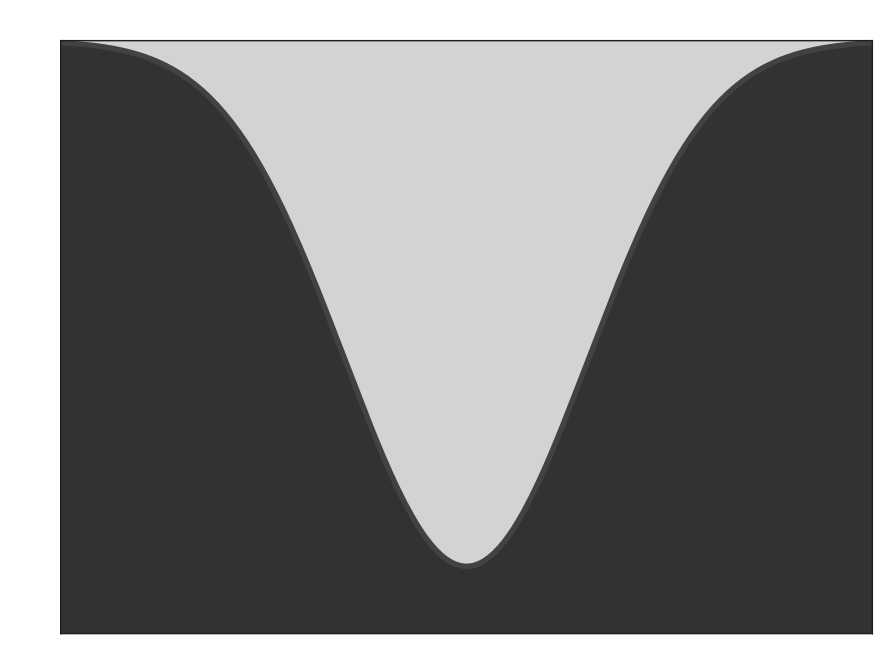
图1.4两个类别(用浅色和深色表示)不能用线分开,需要用曲线分隔符。在三维空间中,这相当于说没有平面可以分开表面;需要一个曲面分隔符。在静止的空间中,这相当于说没有超平面可以分开类别;需要一个弯曲的超曲面。
机器学习中非常流行的非线性函数是Sigmoid函数,因为它看起来像字母 S,所以也叫S 型函数。Sigmoid函数通常用希腊字母𝜎表示。它的定义如下 \(\sigma^2(x)=\frac1{1+e^{-x}}\) (1.5)
图1.5显示了 Sigmoid函数的图形。因此,我们可以使用等式1.6,这是个非常流行的模型架构,叫做逻辑回归(仍然比较简单),该架构采用输入加权和的Sigmoid函数(无参数):
\(y=\sigma\left(\vec{w}^T\vec{x}+b\right) (1.6)\)
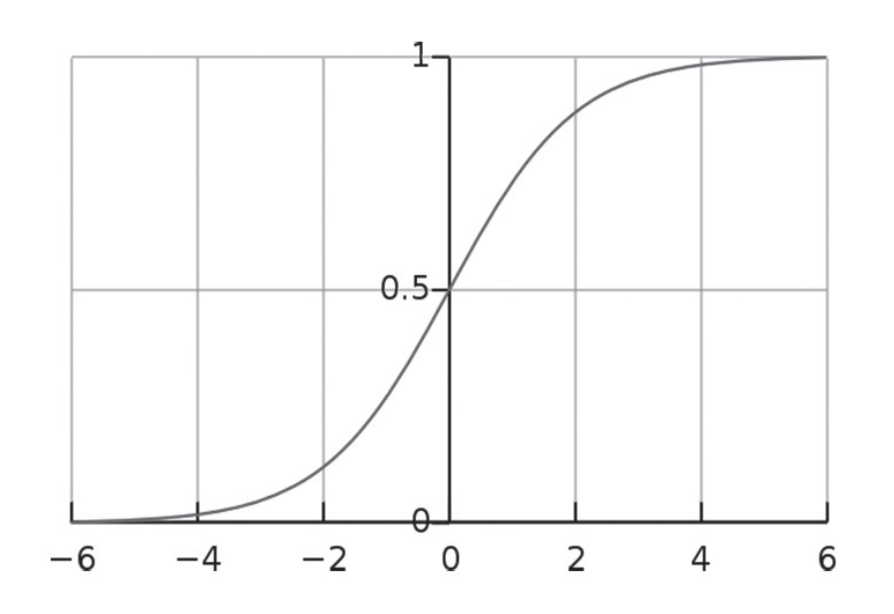
图1.5 Sigmoid函数图形
Sigmoid函数赋予了非线性。与单独的加权和相比,这种架构可以处理相对更复杂的分类任务。事实上,等式1.6描述了神经网络的基本构建块。
1.7 通过多个非线性层实现更高的表达能力:深度神经网络
在第1.6节中,我们指出,在基本加权和模型中添加非线性可以产生能够处理更复杂任务的模型架构。用机器学习术语来说,非线性模型具有更强的表达能力。
现在考虑一个现实生活中的问题:比如,构建一个狗识别器。输入空间包括像素位置和像素颜色(x、y、r、g、b,其中 r、g、b 表示像素颜色的红色、绿色和蓝色成分)。输入维度很大(与图像中的像素数量成比例)。图1.6简要介绍了典型的深度学习系统(例如狗图像识别器)必须处理的背景和前景的可能变化。我们需要一台具有极高表达能力的机器。我们如何以原则性的方式创建这样的机器?

图1.6 非典型深度学习系统(此处为狗图像识别器)需要处理的背景和前景变化一览
与其一步一步地从输入生成输出,不如采用级联方法?我们将从输入中生成一组中间或隐藏输出,其中每个隐藏输出本质上是一个逻辑回归单元。然后我们添加另一层,将前一层的输出作为输入,依此类推。最后,我们将最外层的隐藏层输出合并到总输出中。
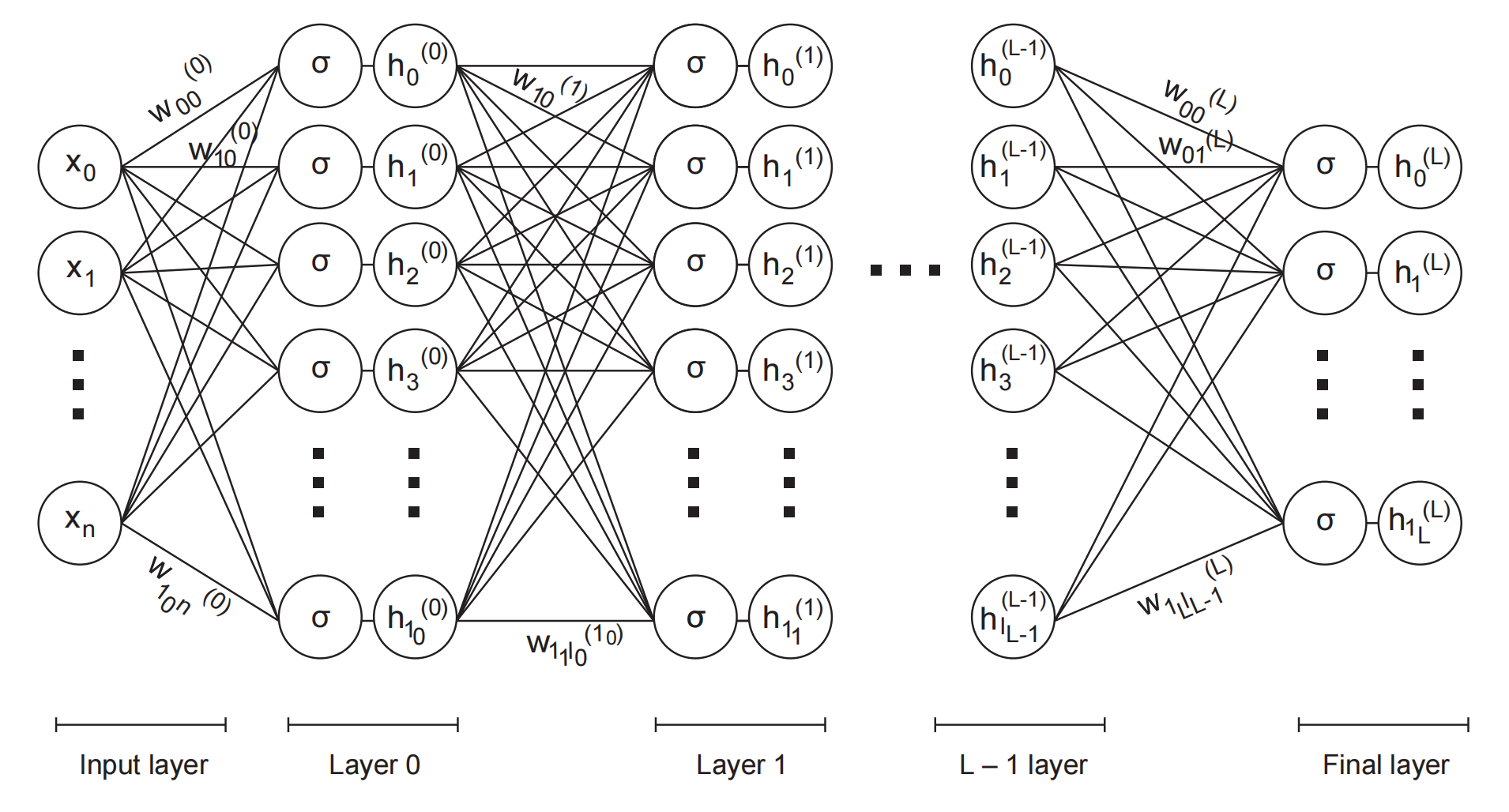
图1.7 多层神经网络
我们用以下等式来描述该系统。请注意,我们在权重上添加了一个上标来标识层(层0 最接近输入;层 L 是最后一层,距离输入最远)。我们还将下标设为二维(因此给定层的权重是一个矩阵)。第一个下标标识目标节点,第二个下标标识源节点(见图1.7)。
精明的读者可能会注意到,以下等式没有明确的偏差项。这是因为,为了简化符号,我们将其并入权重集并假设其中一个输入(例如,\(x_0\)= 1)和相应的权重(例如\(w_0\))是偏差。
第0层:从n+1个输入生成\(n_0\)个隐藏输出
\(\begin{aligned}&h_0^{(0)}&&=\sigma\left(w_{00}^{(0)}x_0+w_{01}^{(0)}x_1+\cdots w_{0n}^{(0)}x_n\right)\\ &h_1^{(0)}&& =\sigma\left(w_{10}^{(0)}x_0+w_{11}^{(0)}x_1+\cdots w_{1n}^{(0)}x_n\right) \\ &h_{n_0}^{(0)}&& =\sigma\left(w_{n_00}^{(0)}x_0+w_{n_01}^{(0)}x_1+\cdots w_{n_0n}^{(0)}x_n\right) \end{aligned}\) (1.7)
第1层:从第0 层的\(n_0\)个隐藏输出生成\(n_1\)个隐藏输出
\(\begin{aligned} &h_0^{(1)}&& =\sigma\left(w_{00}^{(1)}h_0^{(0)}+w_{01}^{(1)}h_1^{(0)}+\cdots w_{0n_0}^{(1)}h_{n_0}^{(0)}\right) \\ &h_1^{(1)}&& =\sigma\left(w_{10}^{(1)}h_0^{(0)}+w_{11}^{(1)}h_1^{(0)}+\cdots w_{1n_0}^{(1)}h_{n_0}^{(0)}\right) \\ &h_{n_1}^{(1)}&& =\sigma\left(w_{n_10}^{(1)}h_0^{(0)}+w_{n_11}^{(1)}h_1^{(0)}+\cdots w_{n_1n_0}^{(1)}h_{n_0}^{(0)}\right) \end{aligned}\)(1.8)
最后一层(L):从前一层\(n_{L-1}\)个隐藏输出生成m+1个可见输出
\(\begin{aligned} h_0^{(L)}& =\sigma\left(w_{00}^{(L)}h_0^{(L-1)}+w_{01}^{(L)}h_1^{(L-1)}+\cdots w_{0n_{L-1}}^{(L)}h_{n_{L-1}}^{(L-1)}\right) \\ h_1^{(L)}& =\sigma\left(w_{10}^{(L)}h_0^{(L-1)}+w_{11}^{(L)}h_1^{(L-1)}+\cdots w_{1n_{L-1}}^{(L)}h_{n_{L-1}}^{(L-1)}\right) \\ \begin{array}{cc}\vdots\\\end{array}&& \\ h_m^{(L)}& =\sigma\left(w_{m0}^{(L)}h_0^{(L-1)}+w_{m1}^{(L)}h_1^{(L-1)}+\cdots w_{mn_{L-1}}^{(L)}h_{n_{L-1}}^{(L-1)}\right) \end{aligned}\) (1.9)
这些等式如图1.7 所示。图1.7 所示的机器可能非常强大,具有巨大的表达能力。我们可以系统地调整其表达能力以适应手头的问题。它是一个神经网络。我们将用本书的其余部分来研究这一点。
小结
在本章中,我们概述了机器学习,并一直延伸到深度学习。我们用玩具猫脑示例说明了这些想法。本章使用了一些数学概念(例如向量),但没有进行适当的介绍,我们鼓励您在介绍向量和矩阵后重新阅读本章。
我们希望您能从本章中得到以下的收获:
- 机器学习是一种完全不同的计算范式。在传统计算中,我们向计算机提供分步指令序列,告诉它要做什么。在机器学习中,我们建立一个数学模型,试图逼近从输入生成分类或估计的未知函数。
- 模型函数的数学性质由分类或估计任务的物理性质和复杂性决定。模型具有参数。参数值是根据训练数据(具有已知输出的输入)估计的。参数值经过优化,以使模型输出尽可能接近训练输入上的训练输出。
- 机器学习模型可以从另一个角度理解,即几何视角,它是将多维输入空间中的点映射到输出空间中的点的变换。
- 分类/估计任务越复杂,近似函数就越复杂。用机器学习术语来说,复杂的任务需要具有更强表达能力的机器。更高的表达能力来自非线性(例如,S 型函数;参见公式1.5)和更简单机器的分层组合。这让我们想到了深度学习,它只不过是一个多层非线性机器。
- 复杂的模型函数通常通过组合较简单的基函数来构建。
请系好安全带:学习乐趣即将变得更加激烈。