本文是基于《深度学习中的数学》一书中的思想,旨在从本文起系列阐述深度学习技术背后的数学原理,给想要对深度学习更进一步了解的读者提供一个可以查阅的底层原理资料。本文共分为四个部分,此为第三部分。
本文的主要内容包括:
- 机器学习的几何视角
- 机器学习中的回归和分类
1.4 机器学习的几何视角
猫脑模型的每个输入都是一个由两个数字组成的数组:\(x_0\)(表示物体的硬度)、\(x_1\)(表示物体的锋利度),或者等效地,一个2 ×1向量\(\vec{x}\)。直觉上,您可以在头脑里想象将输入视为高维空间中的一个点。输入空间通常称为特征空间——一个表示模型要检查的所有特征的空间。在本例中,特征空间维度为2,但在实际问题中,它将有数百、数千或更多。输入的确切维度因问题而异,但它是一个点的直觉仍然存在。
输出\(y\)也应被视为另一个高维空间中的一个点。在猫脑模型问题中,输出空间的维数为1,但在实际问题中,它会更高。然而,通常情况下,输出维数比输入维数小得多。
从几何学上讲,机器学习模型本质上是将特征空间中的一个点映射到输出空间中的一个点。模型在输出空间中执行的分类或估计工作比在特征空间中更容易。具体来说,对于分类工作,属于不同类别的输入点预计会映射到输出空间中的不同簇。
让我们继续使用猫脑模型示例来说明这个想法。如前所述,我们的特征空间是二维的,两个坐标轴\(X_0\)表示硬度,\(X_1\)表示锋利度。3 此二维空间中的各个点用小写的坐标值(\(x_0\),\(x_1\))表示(见图1.2)。如图所示,对威胁评分进行建模的一个好方法是测量与线\(x_0\)+\(x_1\)= 1 的距离。
从坐标几何学来看,在具有坐标轴 \(X_0\) 和 \(X_1\) 的二维空间中,点(a, b)与直线\(x_0\)+\(x_1\)= 1的有符号距离为\(y=\frac{a+b-1}{\sqrt{2}}\)。通过检查\(y\)的符号,我们可以确定输入点属于分隔线的哪一侧。在图1.2 所示的简单情况下,观察告诉我们,威胁分数可以用与对角线\(x_0\)+\(x_1\)−1 = 0 的有符号距离\(y\)来表示。我们可以通过对 \(y\) 进行阈值化来做出逃跑/忽略/接近的决定。接近零的值表示忽略,正值表示逃跑,负值表示接近并发出呼噜声。
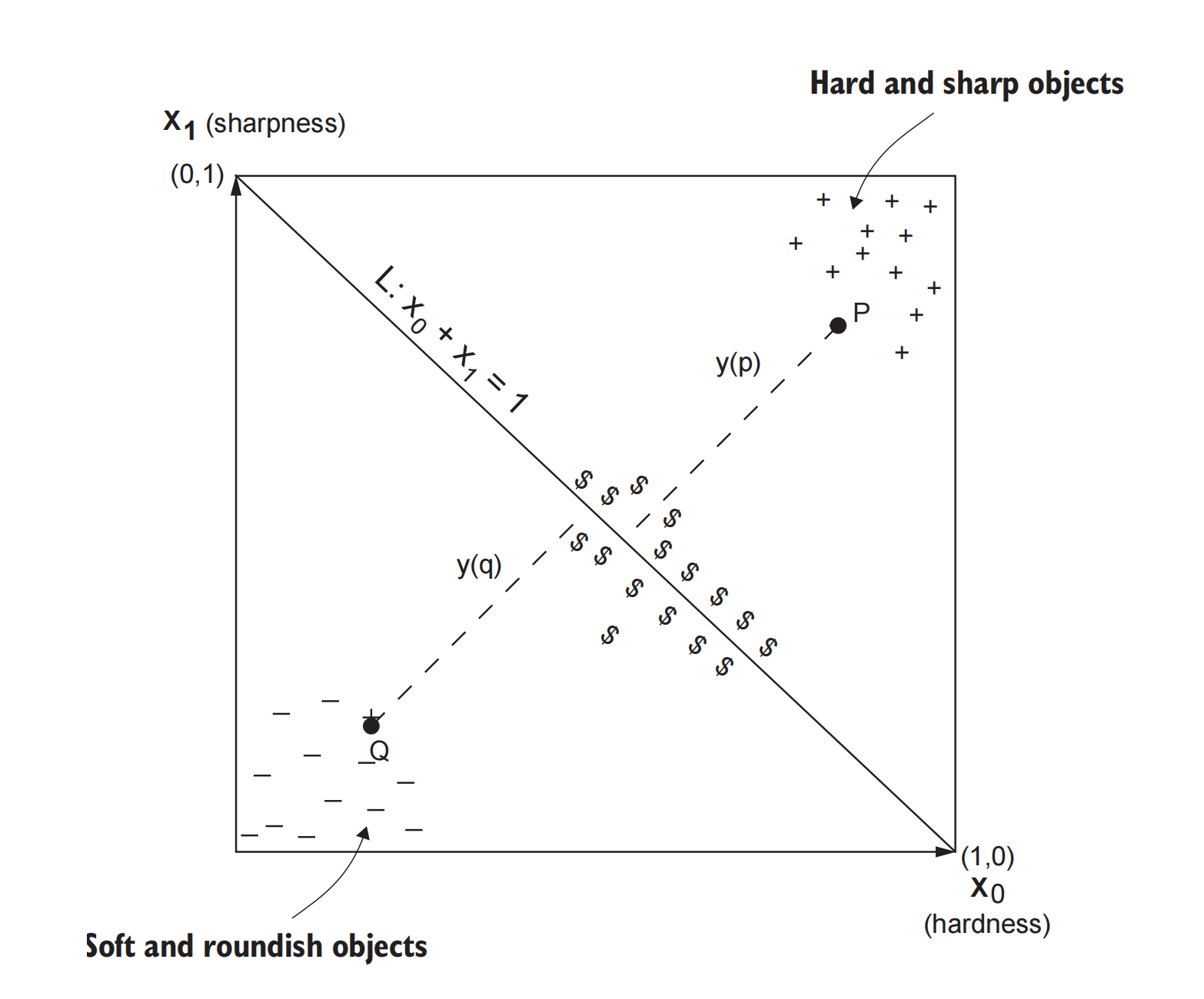
图1.2 猫脑模型的二维输入点空间。左下角显示的是硬度低且锋利度低的物体(-),而右上角显示的是硬度高且锋利度高的物体(+)。中间值在对角线附近($)
第11页脚注:3 我们用\(X_0\)和\(X_1\)作为坐标符号,而不是我们更熟悉的X,Y,这样在进入高维空间时就不会出现符号耗尽的情况。
从高中几何学中可知,任意输入点(\(x_0\)= a,\(x_1\)=$ b\()到直线\)x_0\(+\)x_1\(−1 = 0 的距离为\)\(因此,函数\)y(x_0,x_1)=\(是猫脑威胁估计函数的一个可能模型。训练应收敛到\)w_0=,w_1=和b=-$。 因此,我们简化的猫脑威胁评分模型为
\(y\left(x_0,x_1\right)=\frac1{\sqrt{2}}x_0+\frac1{\sqrt{2}}x_1-\frac1{\sqrt{2}}\)
它将表示猫前方物体硬度和锋利度的二维输入点,映射到与分隔线有符号距离对应的一维值。该距离在物理上可解释为威胁分数,可通过阈值划分类别(负面威胁、中性威胁、正面威胁),如公式1.2 所示。划分的类别在输出空间中形成不同的簇,在输出空间中用+、-和\(\mathbb{\$}\)符号表示。输出值越低,表示负面威胁越确定(猫会靠近并发出呼噜声):例如,\(y\left(0,0\right)=-\frac{1}{\sqrt{2}}\)。输出值越高,表示威胁越大(猫会逃跑):例如,\(y\left(1,1\right)=\frac{1}{\sqrt{2}}\)。中等输入值产生的威胁接近于零(猫会忽略该物体):例如,\(y (0.5,0.5)=0\)。当然,因为问题非常简单,我们可以通过简单的观察得出模型参数。而在现实问题中,这是需要训练的。
几何视角在更高维度上也适用。一般来说,n维输入向量\(\vec{x}\)被映射到m维输出向量(通常 m < n),这样,问题在输出空间中就变得简单得多。图1.3显示了具有三维特征空间的示例。
1.5 机器学习中的回归和分类
如第1.1节简要概述的那样,机器学习模型有两种类型:回归器和分类器。
在回归器中,模型试图在给定特定输入的情况下输出期望值。例如,第1.3 节中猫脑模型的第一阶段(威胁分数估计器)就是回归器模型。
另一方面,分类器有一组预先指定的类。给定一个特定的输入,它们会尝试输出输入所属的类。例如,完整的猫脑模型有三个类:(1)逃跑,(2)忽略,(3)靠近并发出呼噜声。因此,它接受输入(硬度和锐度值)并给出输出决策(又称类)。
在此示例中,我们通过对回归器的输出进行阈值处理将回归器转换为分类器(参见公式1.2)。也可以创建直接输出类的模型,而无需中间的回归器。