本文是基于《深度学习中的数学》一书中的思想,旨在从本文起系列阐述深度学习技术背后的数学原理,给想要对深度学习更进一步了解的读者提供一个可以查阅的底层原理资料。本文共分为四个部分,此为第一部分。
本文的主要内容包括:
- 机器学习/深度学习初探
- 计算范式转变
深度学习已经彻底改变了计算机视觉,尤其是自然语言处理和语音处理,进而改变了整个人工智能领域。人工智能已经从无法令人满意地解决实际问题的浅层技巧,转变成了可以大规模解决行业面临的实际问题的强大工具。这无异于是一场发生在我们眼皮底下的革命。要引领这场革命潮流,不仅仅是简单地记住一些入门指南上的”操作”步骤,还要理解其基本原理和抽象概念。这些至关重要的环节正是数学发挥作用的地方。
在第一章中,我们概述了深度学习。这将要求我们使用后续章节中解释的一些概念。如果本章末尾有一些未解决的问题,请不要担心:它只是旨在引导您的思维先转到我们的主题上来。随着后续章节中各个概念变得更加清晰,您可以考虑回过头来重新阅读本章。
1.1 机器学习/深度学习初探:计算范式转变
做出决定和/或预测是生活的一个核心诉求。这样做在本质上涉及到接收一组感官或知识输入并对其进行处理以生成决策或估计。
例如,猫的大脑经常试图在以下选项之间进行选择:逃离它面前的物体,忽略它面前的物体,接近它面前的物体并发出呼噜声。猫的大脑通过处理感官输入来做出决定,例如感知到的它面前物体的硬度、感知到的它面前物体的锋利度等。这是一个分类问题的例子,其输出是一组可能的类别之一。
生活中的分类问题还有如下的一些其他例子:
根据股票价格历史和近期股票价格变化等输入,判断买入、持有还是卖出某只股票
物体识别(图像): –这是汽车还是长颈鹿? –这是人类还是非人类? –这是无生命物体还是生物? –人脸识别——这是汤姆、迪克、玛丽、爱因斯坦还是梅西?
视频中的动作识别: –这个人是在跑步还是没跑步? –这个人是在捡东西还是没捡东西? –这个人是在做暴力的事情还是没做暴力的事情?
数字文档中的自然语言处理(NLP): –这篇新闻文章属于政治还是体育领域? –这个查询短语是否与档案中的特定文章匹配?
有时生活需要定量估计而不是分类。狮子的大脑需要通过处理猎物的速度和与猎物的距离等输入信息来估计要跳多远才能落在猎物身上。定量估计的另一个例子是根据房主的当前收入、街区的犯罪统计数据等输入信息来估计房价。这种定量估计的工具称为回归器。
以下是日常生活中需要定量估计的其他一些例子:
- 从图像中进行物体定位:识别物体位置的矩形边界
- 根据历史股价和其他新闻事件进行股价预测
- 一对文档之间的相似度得分
有时,分类输出可以从定量估计中生成。例如,前面描述的猫脑可以结合输入(硬度、锋利度等)来生成定量威胁分数。如果威胁分数很高,猫就会逃跑。如果威胁分数接近零,猫就会忽略它面前的物体。如果威胁分数为负,猫就会接近物体并发出呼噜声。 图1.1 显示了许多这样的示例。在每个实例中,机器(即大脑)将感官或知识输入转化为决策或定量估计。机器学习的目标是模拟该机器。
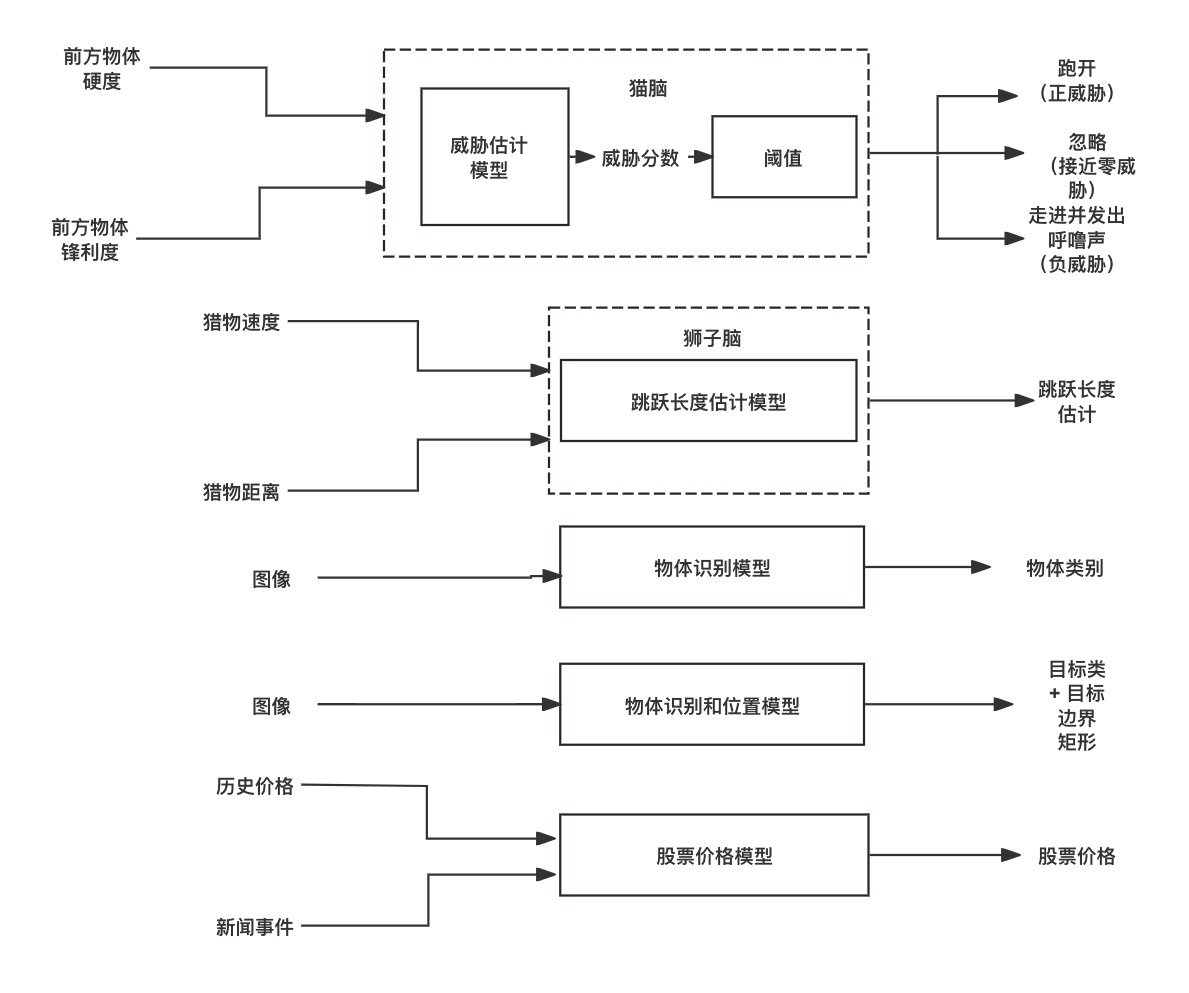
Figure1.1 生活中的决策定量估计模型
请注意,机器学习还有很长的路要走才能赶上人脑。人脑可以独自处理数千甚至数百万个这样的问题。另一方面,在目前的发展状态下,机器学习几乎无法创建一台能够做出所有决策和估计的通用型机器。我们目前主要是试图分别制造单个的机器来针对性解决单个任务(例如选股器或汽车识别器)。此时,您可能会问:“等等,将输入转换为输出——这不正是计算机在过去30 多年里一直在做的事情吗?这里提到的范式转换是什么?”答案是,范式转换就是,我们没有向机器提供分步指令集(即程序)来将输入转换为输出。相反,我们是为该问题开发了一个数学模型。
让我们用一个例子来说明这个想法。为了简单和具体,我们将考虑一个假设的猫脑,它在生活中只需要做出一个决定:是逃离它面前的物体,还是忽略物体,还是走近并发出呼噜声。这个决定就是我们将要讨论的模型的输出。在这个示例中,决定仅基于两个定量输入(又称特征):即感知到的物体的硬度和锋利度(如图1.1 所示)。我们不会通过提供分步指令来实现这一点,例如“如果锐度大于某个阈值,则逃跑”。相反,我们会尝试确定一个参数化函数,该函数接受输入并将其转换为所需的决策或估计值。而最简单的此类函数就是输入的加权和:
y (hardness, sharpness)= w0 ×hardness+w1×sharpness+ b
权重w0、w1 和偏差b是函数的参数。输出y可以解释为威胁分数。如果威胁分数超过阈值,猫就会逃跑。如果接近0,猫就会忽略该物体。如果威胁分数为负,猫就会靠近并发出呼噜声。对于更复杂的任务,我们将使用更复杂的函数。请注意,权重最初是未知的;我们需要估计它们。这是通过称为模型训练的过程完成的。
总体而言,通过机器学习解决问题有以下几个阶段:
- 我们设计一个具有未知参数(权重)的参数化模型函数(例如加权和)。这构成了模型架构。选择正确的模型架构是机器学习工程师的专业知识发挥作用的地方。
- 然后我们通过模型训练估计权重。
- 一旦估计出权重,我们就有了一个完整的模型。这个模型可以接受以前不一定见过的任意输入并生成输出。利用训练好的模型处理任意真实输入并产生输出的过程称为推理。
这个被称为监督学习的过程是最常用的机器学习种类。在这里,我们在开始训练之前要准备好训练数据。训练数据包括示例输入项,每个输入项都有其对应的期望输出。训练数据通常是手动创建的:人工检查每一个输入项并标注好期望输出(又称目标输出)。这通常是机器学习中最艰巨繁琐的部分。
例如,在我们假设的猫脑示例中,一些可能的训练数据样本如下
第4页脚注: 1 如果你有机器学习的经验,你就会意识到我们这里讨论的是“监督”学习。另外还有一种机器学习方式不需要已知输出,即所谓的“无监督”学习,我们稍后会讨论这种方式。
输入:(硬度=0.01,锋利度=0.02)→威胁=-0.90 →决策:“靠近并发出呼噜声“ 输入:(硬度=0.50,锋利度=0.60)→威胁=-0.01 →决策:“忽略“ 输入:(硬度=0.99,锋利度=0.97)→威胁=0.90 →决策:“逃跑“
其中硬度和锋利度的输入值假设介于0 和1 之间。
训练过程中究竟发生了什么?答案:我们迭代处理输入的训练数据样本。对于每个输入项,我们都有期望的(又称目标)输出结果。在每次迭代中,我们都会调整模型权重值,使得模型函数对该特定输入项的输出尽可能地更接近其对应的目标输出。例如,假设在给定的迭代中,权重值为\(w_0\)= 20 和\(w_1\)= 10,\(b\)= 50。在输入(硬度= 0.01,锐度= 0.02)中,我们得到输出威胁分数\(y\)= 50.3,这与我们期望的 y = −0.9 有很大不同。我们将调整权重:例如,减少偏差,使\(w_0\)= 20、\(w_1\)= 10 和$ b\(= 40。那么相应的威胁分数\) y$= 40.3 仍然远未达到期望值,但已经更接近了。在我们对许多训练数据样本执行此操作后,权重将开始接近其理想值。请注意,如何识别对权重值的调整不在此处讨论;它需要更深层次的数学知识,稍后将进行讨论。
如前所述,这种迭代调整权重的过程称为训练或学习。在学习开始时,权重具有随机值,因此机器输出通常与期望输出不匹配。但随着时间的推移,更多的训练迭代发生,机器“学会”了如何生成我们期望的输出。这时模型就可以在现实世界中部署了。给定任意输入,模型将在推理过程中产出更接近人们想要的结果。
仔细想想,这可能就是活体大脑的工作方式。它们包含各种任务的数学模型的等价物。在这里,权重是大脑中不同神经元之间连接(又称突触)的强度。一开始,参数未调整;大脑反复犯错。例如,婴儿的大脑经常在识别可食用物体时犯错误——任何有过孩子的人都能明白我们在说什么。但每个大脑都会调整参数(吃带有$符号的绿色和白色矩形物体会招致很多责骂-以后不应该吃它们,等等)。最终,这台大脑机器会调整好参数以产生更好的结果。
这里应该注意一个微妙的点。在训练过程中,机器会调整其参数,以便仅根据训练数据输入产生所需的结果。当然,在训练过程中,它只看到所有可能输入的一小部分——我们不会构建从已知输入到已知输出的查找表。因此,当这台机器在真实世界发布时,它主要运行在从未见过的输入数据上。我们用什么来保证它会在从未见过的数据上产生期望的结果?坦率地说,没有任何保证。只是,在大多数现实生活的问题中,输入并不是真正随机的。它们会有一个模式。我们希望机器在训练期间能看到足够多的数据来捕捉这种模式。这样它在没有见过的输入上的输出将会接近所需的值。训练数据的分布越接近现实生活,就越有可能实现。